In this post I’ll show how to construct subsets of data which resist being valued (in the sense of the data valuation research program).
Setup
We will work with the cat/dog subset of CIFAR-10. This forms a binary classification task with 10,000 training examples and 2,000 test examples.
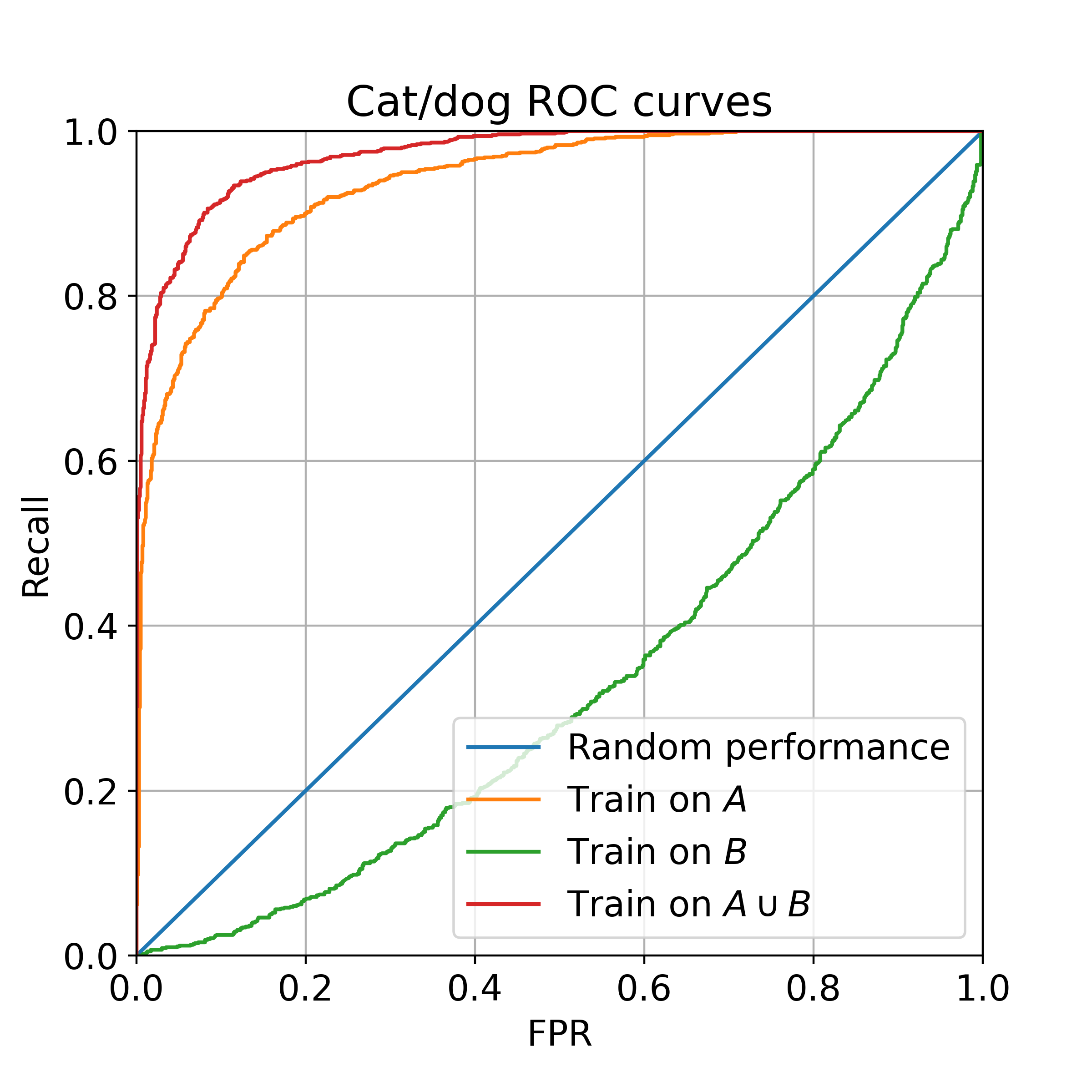
We will construct two subsets of the training data, $A$ and $B$, which yield the following test-set accuracies:
- Train on just $A$: 86% accuracy.
- Train on $A \cup B$: 91% accuracy.
- Train on just $B$: 37% accuracy. (worse than chance!)
Subset $B$ is both beneficial when added to $A$, while also being worse than nothing when used on its own.
This result is problematic for the research program of data valuation – which traditionally “is posed as a problem of equitably splitting the validation performance of a learning algorithm among the training data” (e.g. [1, 2]). What value should we assign to subset $B$? Negative, because it’s worse than nothing on its own? Or positive, because it’s helpful when used alongside $A$? There seems to be no clear answer.
If you are familiar with ROC curves, please enjoy the following.
Method
The construction is as follows.
- Remove a random 10% of the cat/dog training examples, and train a ResNet on this (yields a model with ~75% accuracy).
- Run this model on the remaining 90% of examples.
- Select the top 15% most confident mistakes from this set, as subset $B$.
- Finally, let subset $A$ be the remaining 75% of examples which are not already in $B$.
A notebook which reproduces these results is here. It uses a few extra techniques to slightly pump up the numbers – ensembling and evaluating on augmented images to reduce noise.
Thoughts
Consider any binary classification dataset $S$, paired with any prediction function $f$. I’ll argue that the dataset can always be split into two halves, which on their own cannot give you anything better than $f$.
Let $A$ be the examples in $S$ which are correctly predicted by $f$, and $B$ the mistakes. Then on $A$, $f$ already has perfect accuracy; to additionally realize zero loss, we can simply scale up the logits. And on $B$, the inversion of $f$ (flipping the predictions) likewise has perfect accuracy.
Therefore, when training on either $A$ or $B$ alone, no matter how large and diverse their union is, we cannot rely on ERM to give us a classifier better than $f$ (or its inversion).
It’s only when these two sets (correctly predicted examples & mistakes) are taken together that they can give models better than $f$.
Related work
In Learning from Incorrectly Labeled Data, Eric Wallace presented the following experiment:
- Train on CIFAR-10 (all 10 classes) for 2 epochs, yielding a model with 63% accuracy.
- Run the model on the entire training set of 50,000 points, and relabel according to the model’s prediction.
- Throw out all those examples which were predicted correctly, leaving a set of ~18,500 entirely mislabeled examples.
- Train on this set … => 50% accuracy! (much better than chance)
The construction presented in this post is derived from Eric’s.
References
[1] Kwon and Zou. Beta Shapley: a Unified and Noise-reduced Data Valuation Framework for Machine Learning. arXiv preprint arXiv:2110.14049, 2021.
[2] Just et al. LAVA: Data Valuation without Pre-Specified Learning Algorithms. ICLR 2023.
[3] Ilyas et al. Datamodels: Predicting Predictions from Training Data. ICML 2022.
[4] Wallace. Learning from Incorrectly Labeled Data. Distill 2019.