Update/note (10/19/23): this effect disappears when we keep examples which the simple model gets confidently correct, not just barely correct.
Consider the following experiment.
- Train for 2 epochs on CIFAR-10 cat/dog data, without augmentations.
- Run the resulting model on the training set.
- Take the subset of examples which are correctly predicted.
- Train a new model on this set (for full duration, also without augmentations).
How accurate will the resulting model be?
Result
- The accuracy of the first model is 65.6%.
- The accuracy of the second model is 70.8%.
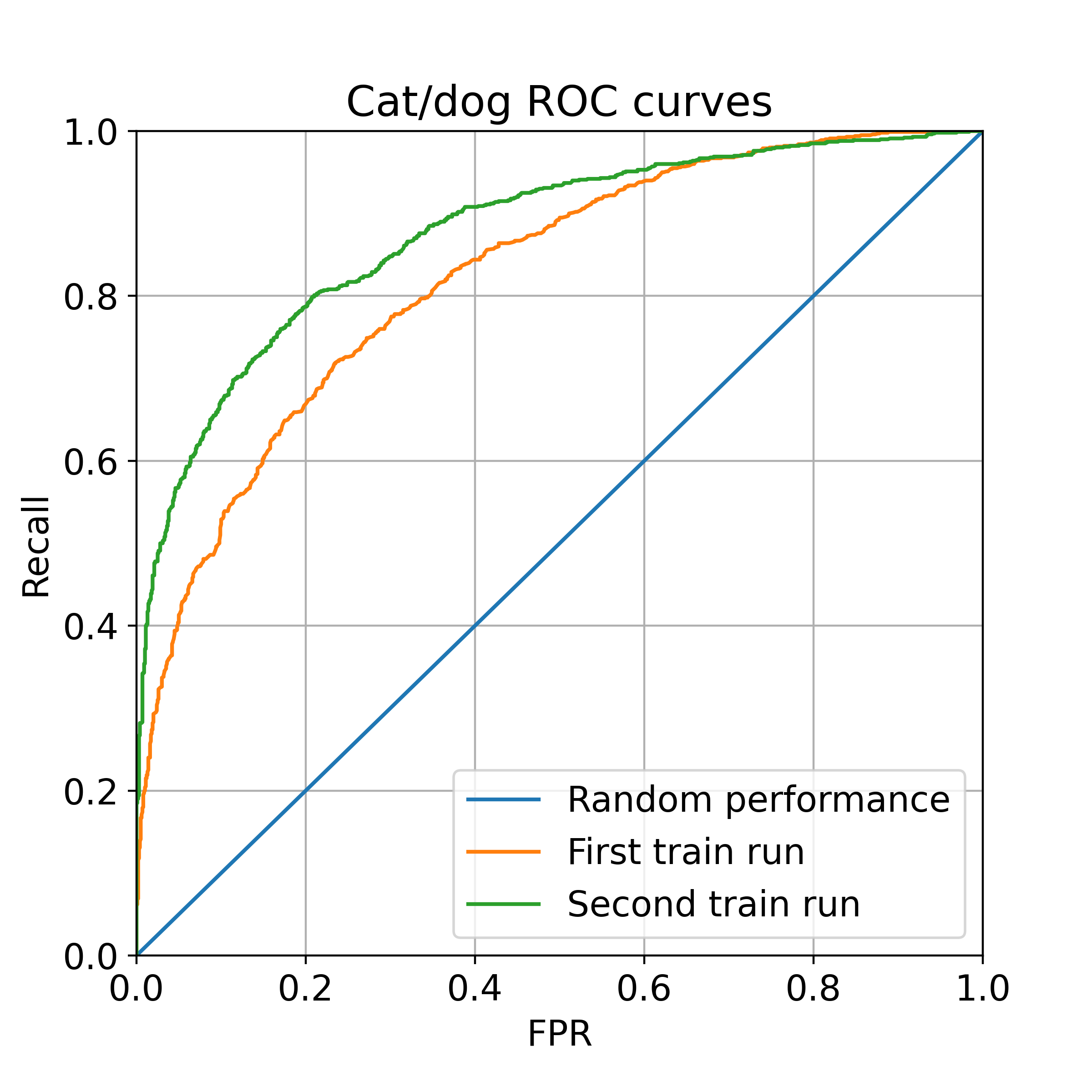
Discussion
Intuitively, it is surprising that the second model is more accurate than the first.
The second run of training should have no reason to learn something better than the first model, which is already 100% accurate on its training data.
So, perhaps this constitutes a demonstration of ‘inductive bias’, where SGD learns a better model than what is “necessary”.
(Note: If we were using data augmentations, then there would be an obvious explanation – in that case, this would be just the same multi-view benefit as utilized in FixMatch, Meta Pseudo Labels, etc. But without data augmentation, these methods don’t work.)
Scaling up
CIFAR-10 is a small (some would say trivial) dataset, especially at the low accuracies in this post. Let’s see what happens when we scale this experiment up.
I’ll be using an internal dataset consisting of 500K pieces of text annotated as positive or negative. The experiment will be analogous to the one above, for BERT models finetuned on this dataset.
- Train a model on 20,000 examples from the dataset.
- Keep only those examples of the remaining 480,000 which the first model already predicts correctly.
- Train a second model on this set.
Result:
- The first model’s validation accuracy is 91.5%.
- The second model’s validation accuracy is 93.4%.
This is significantly better, so we can say that the result replicates when scaling up.
Related Experiments
Here are some related experiments, presented as a Q/A.
- Q: What happens if we only keep examples which are predicted correctly with high confidence? A: This will make the second model much worse.
- Q: What happens if we relabel the entire dataset according to the predictions of the first model, and then train the second model on this? A: The second model won’t surpass the first. (unless we use data augmentation or other training noise)
–
These results are somewhat surprising to me. It’s possible that there’s a simple explanation, but I don’t know it.