Motivation

I am interested in understanding the learning dynamics of neural networks. In particular, I’d like to understand the difference between the neural network “NTK parametrization” and the “mu Parametrization” (the latter from the Tensor Programs series of papers).

I understand that both parametrizations are justified by various analyses of the behavior of training as the width goes to infinity. It is known that the NTK parametriation can essentially already fit any finite amount of data perfectly. So my suspicion is that the difference in power between any two parametrizations must be found in the regime where the amount of data goes to infinity alongside the width. (However this could be totally wrong because I haven’t actually studied Tensor programs yet. Either way, I’m interested in studying this.)

In this note I’ll analyze the simplest possible neural network, an MLP with a single hidden layer using NTK parametrization, as both its width and amount of data go to infinity. I will prove that we remain in the kernel/lazy/linearized regime when the amount of data is below the fourth-root of the width.

My proof is not very sophisticated: it doesn’t use any tools more powerful than Chernoff bounds. I do not know whether this result, or perhaps something better, can already be found in the literature, because I did not do a thorough literature review.

Setup: single layer MLP

Given an input $x \in {\mathbb R}^{d_0}$, the output of an MLP with a single hidden layer, which is using the “NTK parametrization,” is:

$$f_x(W) := \tfrac{1}{\sqrt d_1}W^{(2)}\sigma(\tfrac{1}{\sqrt d_0} W^{(1)}x)$$

where $W^{(2)} \in {\mathbb R}^{1 \times d_1}$ and $W^{(1)} \in {\mathbb R}^{d_1 \times d_0}$ are its weight matrices, which are both initialized IID with zero mean and unit variance.

We assume that the initialization distribution of $W^{(1)}$ is standard Gaussian, and $W^{(2)}$ is either Gaussian or bounded. We also assume that the activation function has bounded second moment and is Lipschitz. Without loss of generality, let $C > 0$ be a constant such that $|\sigma’’(z)| \leq C$ and $|\sigma’(z)| \leq C$ and $|\sigma(z)| \leq C(1+|z|)$. E.g., this covers sigmoid, arbitrarily-smoothed-ReLU, and GELU activations.

Let $X \in {\mathbb R}^{d_0 \times N}$ be our dataset of inputs to the MLP. When the MLP has weights $W$, we write $G(W) \in {\mathbb R}^{d_1(1+d_0) \times N}$ to denote the matrix of gradients of the output with respect to each of the $N$ inputs in the dataset. That is, $G(W)_{:n} := \nabla f_{x^{(n)}}(W)$, where $x^{(n)} = X_{:n}$ is the $n$th column of $X$. We additionally write $K(W) := G(W)^\top G(W)$ to denote the $N \times N$ matrix of dot products between the gradients. We assume that the norm of each datapoint is bounded by $\sqrt d_0$.

We will hold the input dimension $d_0$ fixed, and analyze the training dynamics as the hidden dimension $d_1$ (also known as the width of the MLP) and the number of datapoints $N$ both go to infinity.

We assume at the outset that the data rate is at most linear in the width, that is, $N = O(d_1)$. In fact, it will have to grow much more slowly than this.

We write $\tilde O(x)$ to denote a function which asymptotically grows at most at the rate $x\log^k x$ for some $k \in {\mathbb N}$. And we write $\tilde o(x)$ to denote a function which asymptotically grows more slowly than $x/\log^k x$ for every $k \in {\mathbb N}$. Hence, e.g., $\tilde O(1) \cdot \tilde o(1) = \tilde o(1)$.

Throughout the proofs, if we write $\|A\|_\infty$ where $A$ is a matrix, we mean $\|\mathrm{vec}(A)\|\infty$, i.e., $\max |A_{ij}|$, rather than any other notion of $L^\infty$ norm.

Main result and proof outline

In this note I will prove the following.

Given a randomly initialized wide MLP with a single hidden layer, and a dataset of $N = \tilde o(width^{1/4})$ inputs alongside arbitrary bounded regression targets, we can take $T = \tilde O(N)$ full-batch gradient descent steps with learning rate $\eta = \tilde O(1/T)$ per step, without leaving the linearized regime. That is, in this regime, the trajectory of the model’s outputs can be asymptotically-perfectly predicted using only the angles between the inputs plus the model’s outputs at initialization. In addition, if the inputs are orthogonal, then performing $\omega(N)$ descent steps will perfectly solve the problem.

The key points in the proof are as follows:

  1. NTK convergence theorem: As long as $N$ is polynomial in $d_1$, all the $N^2$ dot products between gradients at initialization are almost-surely equal to the NTK plus a $\tilde O(d^{-1/2})$ error term.
  2. Hessian analysis: The MLP’s Hessian has spectral norm $\tilde O(d_1^{-1/2})$, both at initialization, and anywhere along any optimization trajectory given by taking at most $T = O(N)$ update steps with learning rate $\tilde O(1/T)$ per example across a dataset of $N = O(\sqrt d_1)$ examples.
  3. Discrepancy analysis: A full-batch gradient update with $\tilde O(1)$ learning rate on $N$ points has norm $\tilde O(N)$ (this can be sharp even if the inputs are orthogonal). At curvature $\tilde O(d^{-1/2})$, this induces a discrepancy of order $\tilde O(Nd^{-1/2})$ in the angle of gradients (relative to what they are at initialization, which is roughly the NTK). This discrepancy in angle gets magnified by the size of the step to produce a final discrepancy in values of $\tilde O(N^2d^{-1/2})$.
  4. Trajectory linearization theorem: Therefore, if we limit the dataset size to $N = \tilde o(d_1^{1/4})$, then the discrepancy stays $\tilde o(1)$ and we can perfectly predict the dynamics of gradient descent with $\tilde O(1)$ total learning rate per example spread out over $\tilde O(N)$ steps.
  5. Application to regression: This yields a formula for the dynamics of gradient descent against squared-error loss, which involves only the NTK and the model’s initial outputs.

Gradient kernel

Basic calculation

Given an input $x$, the Jacobian of the first layer’s output (i.e., $\tfrac{1}{\sqrt d_0} W^{(1)}x$) with respect to the MLP’s output is

$$\tfrac{1}{\sqrt d_1}W^{(2)}\mathrm{diag}(\sigma'(\tfrac{1}{\sqrt d_0} W^{(1)}x))$$

Thus, the partial derivatives are:

\begin{align*} \tfrac{\partial f_x(W)}{\partial W_{ij}^{(1)}} &= \left(\tfrac{1}{\sqrt d_1}W_{1i}^{(2)} \cdot \sigma'(\tfrac{1}{\sqrt d_0} W_i^{(1)}x)\right) \cdot \left(\tfrac{1}{\sqrt d_0} x_j\right) \\ \tfrac{\partial f_x(W)}{\partial W_{1i}^{(2)}} &= \tfrac{1}{\sqrt d_1} \sigma(\tfrac{1}{\sqrt d_0} W_i^{(1)}x) \end{align*}

And the gradients are:

\begin{align*} \nabla_{W^{(1)}}f_x(W) &= \left(\tfrac{1}{\sqrt d_1}W^{(2)}\mathrm{diag}(\sigma'(\tfrac{1}{\sqrt d_0} W^{(1)}x))\right)^\top (\tfrac{1}{\sqrt d_0}x)^\top \\ \nabla_{W^{(2)}}f_x(W) &= \tfrac{1}{\sqrt d_1}\sigma(\tfrac{1}{\sqrt d_0} W^{(1)}x) \end{align*}

Therefore, the dot products between the gradients for two inputs $x, \tilde x$ are:

\begin{align*} \langle \nabla_{W^{(1)}}f_x(W), \nabla_{W^{(1)}}f_{\tilde x}(W) \rangle &= \tfrac{1}{d_0}\langle x, \tilde x\rangle \cdot \tfrac{1}{d_1}\sum_{i=1}^{d_1}(W_{1i}^{(2)})^2 \sigma'(\tfrac{1}{\sqrt d_0} W^{(1)}x)\sigma'(\tfrac{1}{\sqrt d_0} W^{(1)}\tilde x) \\ \langle \nabla_{W^{(2)}}f_x(W), \nabla_{W^{(2)}}f_{\tilde x}(W) \rangle &= \tfrac{1}{d_1}\langle \sigma(\tfrac{1}{\sqrt d_0} W^{(1)}x), \sigma(\tfrac{1}{\sqrt d_0} W^{(1)}\tilde x)\rangle \end{align*}

We denote the activations across the dataset $X$ by $F := \sigma(\tfrac{1}{\sqrt d_0}W^{(1)}X)$ and their derivatives by $F’ := \sigma’(\tfrac{1}{\sqrt d_0}W^{(1)}X)$, the full matrix of dot products between their gradients is

$$K = \frac{X^\top X}{d_0} * \frac{F'^\top \mathrm{diag}(W^{(2)})^2 F'}{d_1} + \frac{F^\top F}{d_1}$$

where $*$ denotes element-wise multiplication of matrices.

Moments of the relevant distributions

The entries of $\frac{X^\top X}{d_0}$ are fixed as we increase $d_1$. The entries of $\frac{F’^\top \mathrm{diag}(W^{(2)})^2 F’}{d_1}$ and $\frac{F^\top F}{d_1}$ are both averages of IID variables. To get large deviation bounds for them we now calculate the moments of those variables.

The weights $W^{(1)}$ are initialized using IID Gaussian variables, so given two inputs $x, \tilde x$ from the columns of $X$, if we define $z := \tfrac{1}{\sqrt d_0}W^{(1)}x$ and likewise $\tilde z$, then $(z, \tilde z)$ are jointly Gaussian with distribution ${\mathcal N}(0, \tfrac{1}{d_0} (x, \tilde x)^\top (x, \tilde x))$.

Therefore, the moments that we are interested in calculating are of variables with distribution $Y := \sigma(z)\sigma(\tilde z)$ and $Y’ := \sigma’(z)\sigma’(\tilde z)$.

The conditions we placed on $\sigma$ imply that $|Y| \leq C^2(1+|z|)(1+|\tilde z|)$. Therefore ${\mathbb E}[|Y|^k] \leq C^{2k}{\mathbb E}[(1+|z|)^{2k}]$ where $z$ is the variable among $(z, \tilde z)$ with the larger variance. If $|z| \geq 1$ then $(1 + |z|) \leq 2|z|$. Else if $|z| \leq 1$ then $(1 + |z|) \leq 2$. Therefore either way, $(1 + |z|)^{2k} \leq 2^{2k} + (2|z|)^{2k} = 2^{2k}(1 + (z^2)^k)$. Hence

\begin{align*} {\mathbb E}[|Y|^k] &\leq (2C)^{2k}(1+{\mathbb E}[z^{2k}]) \\ &= (2C\max(\tfrac{1}{\sqrt d_0}\|x\|, \tfrac{1}{\sqrt d_0}\|\tilde x\|))^{2k}(1 + {\mathbb E}[w^{2k}]) \\ &\leq (2C)^{2k}(1 + (2k-1)!!) \\ &\leq (2C)^{2k}(1 + (2k)!!) \\ &= (2C)^{2k}(1 + 2^kk!) \\ &\leq (3C)^{2k}k! \\ \end{align*}

where we use our assumption that $\|x\| \leq \sqrt d_0$, and the formula for the $2k$th moment of a Gaussian.

We have therefore shown that the IID distributions whose averages make up the entries of the term $\frac{F^\top F}{d_1}$ each have moments bounded by $(3C)^{2k}k!$.

For the matrix $\frac{F’^\top \mathrm{diag}(W^{(2)})^2 F’}{d_1}$, its entries are averages of variables of distribution $w^2Y’$, where $w \sim {\mathcal N}(0, 1)$ stands in for one of the IID $W_{1i}^{(2)}$. This satisfies

$${\mathbb E}[(w^2Y')^k] \leq {\mathbb E}[w^{2k}]{\mathbb E}[|Y'|^k] \leq {\mathbb E}[w^{2k}]C^{2k} = (2k-1)!!C^{2k} \leq (3C)^{2k}k!$$

Therefore, the distributions in the IID averages forming the entries of both matrices always have their $k$th moment bounded by $(9C^2)^kk!$.

Deviation bound

We previously proved that the $N \times N$ matrices $\frac{F’^\top \mathrm{diag}(W^{(2)})^2 F’}{d_1}$ and $\frac{F^\top F}{d_1}$ have entries which are each an average of $d_1$ IID variables whose distribution has $k$th moment bounded by $(9C^2)^kk!$. Therefore, via generic sub-exponential large deviation bounds, we have

$$P\left(\max_{(i, j) \in [N]^2} |M_{ij} - {\mathbb E}[M_{ij}]| \geq a\right) \leq N^2 e^{-d_1(0.08(a/(9C^2)))} \leq N^2e^{-d_1\tfrac{0.008a^2}{C^2}}.$$

In particular, letting $a = (C^2/0.008)d_1^{-1/2}\log^2 d_1$, and using the assumption that $N = O(d_1)$, we have

$$N^2e^{-d_1\tfrac{0.008a^2}{C^2}} = O(d_1^2)e^{-\log^4d_1} = O(d_1^2 d_1^{-4}) = O(d_1^{-2})$$

and therefore

$$\sum_{d_1=1}^\infty P\left(\max_{(i, j) \in [N]^2} |M_{ij} - {\mathbb E}[M_{ij}]| \geq (C^2/0.008)d_1^{-1/2}\log^2 d_1\right) < \infty$$

hence almost-surely $\|M - {\mathbb E}[M]\|_\infty = \tilde O(d_1^{-1/2})$, where $\tilde O$ ignores logarithmic factors, and $M$ ranges over both of the two matrices.

Calculation of the expectations

It remains to calculate the expectations ${\mathbb E}[M]$ for matrices $\frac{F’^\top \mathrm{diag}(W^{(2)})^2 F’}{d_1}$ and $\frac{F^\top F}{d_1}$.

Let $X_{:n_1} = x$ and $X_{:n_2} = \tilde x$. Then for any $j \in \{1, \dots, d_1\}$, the variables $z := \tfrac{1}{\sqrt d_0} W_j^{(1)}$ and likewise $\tilde z$ are jointly Gaussian with covariance given by

\begin{align*} {\mathbb E}[z \tilde{z}] &= {\mathbb E}\left[\frac{1}{d_0} (W_j^{(1)} x)(W_j^{(1)} \tilde{x})\right] \\ &= {\mathbb E}\left[\frac{1}{d_0} \sum_{i_1=1}^{d_0} \sum_{i_2=1}^{d_0} (W_{ji_1}^{(1)} x_{i_1})(W_{ji_2}^{(1)} \tilde x_{i_2})\right] \\ &= \frac{1}{d_0} \sum_{i_1=1}^{d_0} \sum_{i_2=1}^{d_0}{\mathbb E}\left[(W_{ji_1}^{(1)} x_{i_1})(W_{ji_2}^{(1)} \tilde x_{i_2})\right] \\ &= \frac{1}{d_0} \sum_{i_1=1}^{d_0} \sum_{i_2=1}^{d_0} (x_{i_1}\tilde x_{i_2}){\mathbb E}\left[W_{ji_1}^{(1)}W_{ji_2}^{(1)}\right] \\ &= \frac{1}{d_0} \sum_{i_1=1}^{d_0} \sum_{i_2=1}^{d_0} (x_{i_1}\tilde x_{i_2})1\{i_1=i_2\} \\ &= \frac{1}{d_0} \sum_{i=1}^{d_0} x_i\tilde x_i \\ &= \tfrac{1}{d_0} \langle x, \tilde x \rangle. \end{align*}

Therefore, according to the definition of the dual of the activation $\sigma$, we have

$${\mathbb E}[\tfrac{F^\top F}{d_1}] = \mathring{\sigma}(\tfrac{1}{d_0}X^\top X)$$

We next calculate ${\mathbb E}[\frac{F’^\top \mathrm{diag}(W^{(2)})^2 F’}{d_1}]$. We have:

\begin{align*} {\mathbb E}\left[(\tfrac{F'^\top \mathrm{diag}(W^{(2)})^2 F'}{d_1})_{n_1n_2}\right] &= {\mathbb E}\left[\frac{1}{d_1}\sum_{i=1}^{d_1} (W_{1i}^{(2)})^2 \sigma'(\tfrac{1}{\sqrt d_0} W_i^{(1)} x)\sigma'(\tfrac{1}{\sqrt d_0} W_i^{(1)} \tilde x)\right] \\ &= {\mathbb E}_{z, \tilde z \sim {\mathcal N}(0, \tfrac{1}{d_0}(x, \tilde x)^\top (x, \tilde x))}\left[\sigma'(z)\sigma'(\tilde z)\right] \\ \end{align*}

and therefore

$${\mathbb E}\left[\tfrac{F'^\top \mathrm{diag}(W^{(2)})^2 F'}{d_1}\right] = \mathring{\sigma'}(\tfrac{1}{d_0}X^\top X)$$

NTK convergence theorem

Define the neural tangent kernel given a matrix of dot products $\Sigma \in {\mathbb R}^{N \times N}$ via

$$\mathrm{NTK}(\Sigma) = \Sigma * \mathring{\sigma'}(\Sigma) + \mathring{\sigma}(\Sigma)$$

The following theorem states that the dot products between gradients are asymptotically given by the neural tangent kernel, at a uniform rate of convergence across all pairs in the dataset.

Theorem. Let $W$ be the initialization weights of the MLP. Then $K(W) = G(W)^\top G(W)$ satisfies:

$$P\left(\|K(W) - \mathrm{NTK}(\tfrac{1}{d_0}X^\top X)\|_\infty = \tilde O(d_1^{-1/2})\right) = 1$$

Proof. This is immediate from the previous section.

In the case that $\|x\| = \sqrt d_0$ for every column of $X$, hence $\tfrac{1}{d_0}X^\top X$ has unit diagonal, we can overload the definition of $\mathrm{NTK}$ via

$$\mathrm{NTK}(\kappa) = \kappa \cdot \mathring{\sigma'}(\kappa) + \mathring{\sigma}(\kappa)$$

for every angle $\kappa \in [-1, 1]$.

According to our second proposition regarding duals (in the Appendix), if this conditions is satisfied, then this definition of the NTK is consistent with the full-matrix one when applied element-wise.

Intuition for this NTK formula:

  • Every single filter (row) of the first layer has a gradient which is some scalar times the input. The question is just what the scalar will be, which depends on the derivative of the activation function.
  • Therefore the dot product of gradients in the first layer will just be the dot product between the inputs, times the expected product of the two activation-derivatives wrt the two different inputs. For ReLU, this latter quantity is precisely the fraction of neurons which are co-activated across both inputs.
  • The final weight’s gradient is always just the hidden activations. So the dot product in the final layer is proportional to the dot product of hidden activations.

Concrete values and visualization for ReLU

Theorem. If $\sigma(x) = \sqrt 2 \max(0, x)$, and $\|x\| = \|\tilde x\| = \sqrt d_0$ and $\langle x, \tilde x\rangle = \kappa d_0$, then:

$$\mathrm{NTK}(\kappa) = \kappa + \tfrac1\pi\sqrt{1 - \kappa^2} + \tfrac{2\kappa}{\pi}\left(\sin^{-1}\sqrt{\tfrac{1+\kappa}{2}} - \sin^{-1}\sqrt{\tfrac{1-\kappa}{2}}\right).$$

Proof. Combination of previous theorem with formulas for ReLU and ReLU’.

The kernel $\mathrm{NTK}_{\mathrm{ReLU}}(\kappa)$ looks like:

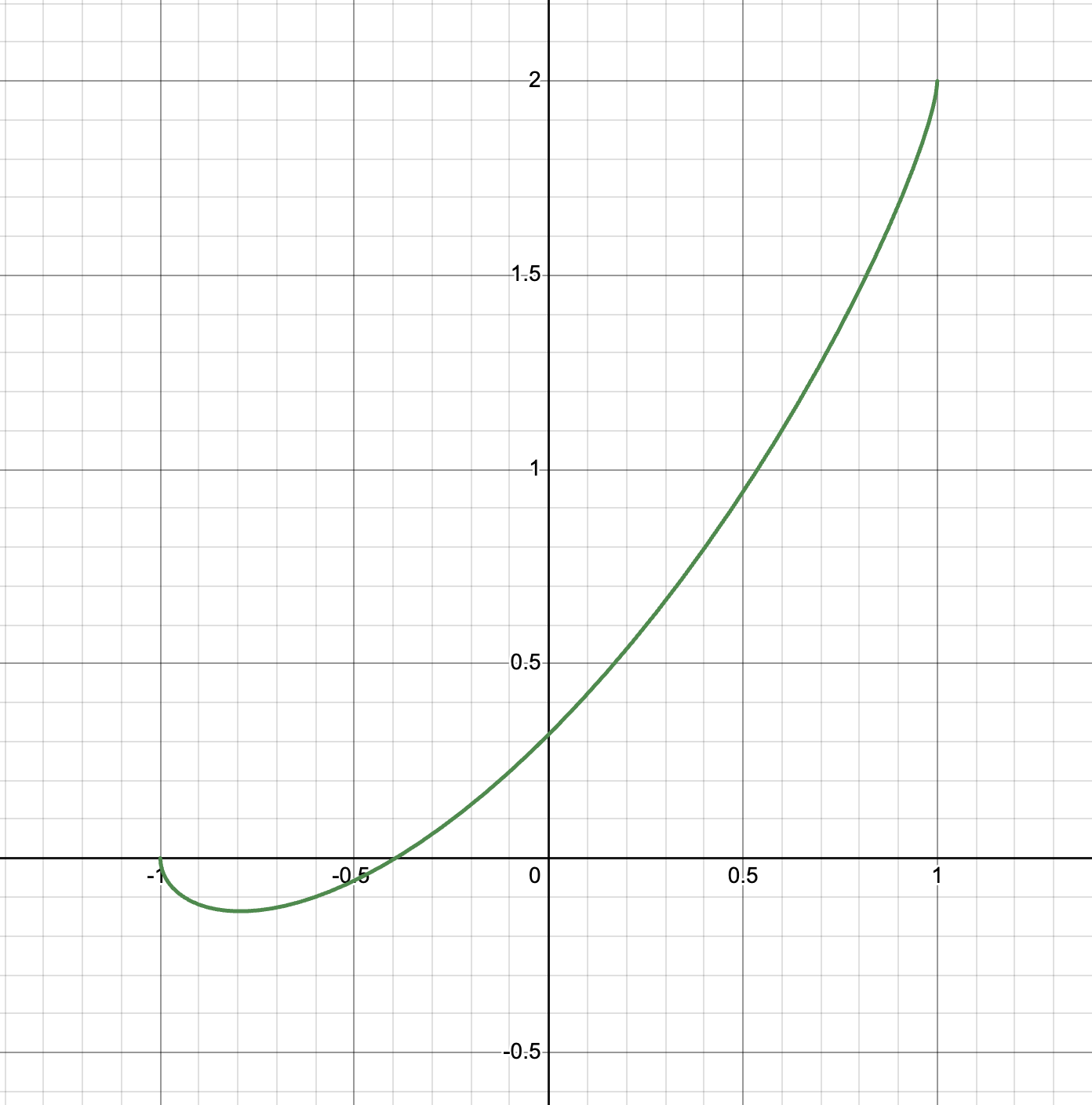
This is actually correct (confirmed by simulation). In particular, single hidden layer ReLU MLPs have the property that, if you have two inputs which are almost opposites of each other, and you want them to “look more different”, then you should make them a bit closer to each other. One is reminded of the GELU activation.

BTW, if you’re lazy and don’t wanna do the calculus to derive the duals, it’s perfectly correct to just compute them via simulation, i.e., generate a stream of Gaussian samples with the correct covariance, and then just compute the expectation in the formula for the dual. This would look something like the following.

import torch

xx1 = torch.randn(5000000, device='cuda')
xx2 = torch.randn(5000000, device='cuda')

def dual(fn, kappa):
    gamma = ((1 - kappa) / 2)**0.5
    yy1 = (1 - gamma**2)**0.5 * xx1 + gamma * xx2 
    yy2 = (1 - gamma**2)**0.5 * xx1 - gamma * xx2 
    assert (0.998 < (yy1 * yy1).mean() < 1.002)
    assert ((yy1 * yy2).mean() - kappa) < 0.002
    return (fn(yy1) * fn(yy2)).mean()

def prime(x, act):
    p = torch.nn.Parameter(x)
    y = act(p)
    y.sum().backward()
    return p.grad

def ntk(kappa, act):
    return kappa * dual(lambda x: prime(x, act), kappa) + dual(act, kappa)

print(ntk(-0.8, torch.relu)) # -0.0684

To see that the kernel has value zero at $\kappa = -1$ (i.e., when the two inputs are opposite), visualize that their two sets of activated neurons, and therefore also their sets of weights with any gradient, will be disjoint.

Whereas to see that the value is negative at $\kappa = -0.9$, visualize that some percent of neurons will be activated by both inputs (in fact, exactly $\mathring{\mathrm{ReLU}}’(-0.9)$ many), and their incoming weights will have almost opposite gradients, so the two inputs will overall have gradients which point in somewhat opposite directions.

Hessian and asymptotic linearization

The kernel we have derived applies only to the initialization-time behavior of the network and its gradients. To extend it to the train-time behavior (i.e., after we take one or more gradient steps), our next step is to analyze the Hessian.

Hessian: Basic calculation

The MLP’s gradients are:

$$\frac{\partial h_1^{(2)}}{\partial W_{ij}^{(1)}} = \left(\tfrac{1}{\sqrt{d_1}}W_{1i}^{(2)}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}a)\right)(\tfrac{1}{\sqrt{d_0}}a_j)$$
$$\frac{\partial h_1^{(2)}}{\partial W_{1i}^{(2)}} = \tfrac{1}{\sqrt{d_1}}\sigma(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}a)$$

Most weights do not affect the gradients of other weights. In particular, none of the rows of $W^{(1)}$ affect any of the other rows. And between $W^{(2)}$ and $W^{(1)}$, only $W_{1i}^{(2)}$ interacts with $W_i^{(1)}$. Changes to $W^{(2)}$ do not affect its own gradient. So the only nonzero interactions are:

$$\frac{\frac{\partial h_1^{(2)}}{\partial W_{1i}^{(2)}}}{\partial W_{ij}^{(1)}} = \frac{\frac{\partial h_1^{(2)}}{\partial W_{ij}^{(1)}}}{\partial W_{1i}^{(2)}} = \left(\tfrac{1}{\sqrt{d_1}}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}a)\right)(\tfrac{1}{\sqrt{d_0}}a_j)$$
$$\frac{\frac{\partial h_1^{(2)}}{\partial W_{ij_1}^{(1)}}}{\partial W_{ij_2}^{(1)}} = \left(\tfrac{1}{\sqrt{d_1}}W_{1i}^{(2)}\sigma''(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}a)\right)(\tfrac{1}{\sqrt{d_0}}a_{j_1})(\tfrac{1}{\sqrt{d_0}}a_{j_2})$$

Hessian: spectral norm

Theorem. If $\|\tfrac{1}{\sqrt d_0}x\|^2 \leq 1$, then the spectral norm of the Hessian is bounded by:

$$\|D^2f_x(W)\|_* \leq \sqrt{2}Cd_1^{-1/2} (1+\|W^{(2)}\|_\infty)$$

Proof. The spectral norm of the Hessian is given by

$$\|D^2f_x(W)\|_* = \sup_{U: \|U\|_F \leq 1} \|(D^2f_x(W))U\|_F$$

where $U = (U^{(2)}, U^{(1)})$ is an arbitrary weight update with bounded $L^2$ norm. The matrix $(D^2f_a(W))U$, which describes the local impact of the update $U$ on the network’s gradient, can be decomposed into a series of sub-blocks based on parts of the gradient.

We first calculate the local impact of $U$ on the gradient with respect to $W_{1i}^{(2)}$:

\begin{align*} (D_WD_{W_{1i}^{(2)}} f_x(W)) U &= \sum_{j=1}^{d_0} D_{W_{ij}^{(1)}}D_{W_{1i}^{(2)}}f_x(W)U_{ij}^{(1)} \\ &= \sum_{j=1}^{d_0} \left(\tfrac{1}{\sqrt{d_1}}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\right)(\tfrac{1}{\sqrt{d_0}}x_j) U_{ij}^{(1)} \\ &= \tfrac{1}{\sqrt{d_1}}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\tfrac{1}{\sqrt{d_0}} U_ix \end{align*}

Therefore we have:

\begin{align*} \|(D_WD_{W^{(2)}} f_x(W)) U\|_F^2 &= \sum_{i=1}^{d_1} (D_WD_{W_{1i}^{(2)}} f_x(W)U)^2 \\ &= \sum_{i=1}^{d_1} \left(\tfrac{1}{\sqrt{d_1}}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\tfrac{1}{\sqrt{d_0}} U_ix\right)^2 \\ &= \frac{1}{d_1}\sum_{i=1}^{d_1} (\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x))^2(\tfrac{1}{\sqrt{d_0}} U_ix)^2 \\ &\leq \frac{1}{d_1}\sum_{i=1}^{d_1} C^2(\tfrac{1}{\sqrt{d_0}} U_ix)^2 \\ &= \tfrac{1}{d_1}C^2\|\tfrac{1}{\sqrt{d_0}} Ux\|_2^2 \\ &\leq \tfrac{1}{d_1}C^2 \end{align*}

where we used the assumption that $\|x\| \leq \sqrt{d_0}$ and $\|U\|_F \leq 1$.

We next calculate the local impact of $U$ on the partial derivative of $W_{ij_1}^{(1)}$:

\begin{align*} &(D_WD_{W_{ij_1}^{(1)}}f_x(W))U = (D_{W_{1i}^{(2)}}D_{W_{ij_1}^{(1)}}f_x(W))U_{1i}^{(2)} + \sum_{j_2=1}^{d_0} (D_{W_{ij_2}^{(1)}}D_{W_{ij_1}^{(1)}}f_x(W))U_{ij_2}^{(1)} \\ &= \left(\tfrac{1}{\sqrt{d_1}}\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\right)(\tfrac{1}{\sqrt{d_0}}x_{j_1}) U_{1i}^{(2)} \\ &\quad\quad+ \sum_{j_2=1}^{d_0} \left(\tfrac{1}{\sqrt{d_1}}W_{1i}^{(2)}\sigma''(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\right)(\tfrac{1}{\sqrt{d_0}}x_{j_1})(\tfrac{1}{\sqrt{d_0}}x_{j_2})U_{ij_2}^{(1)} \\ &= \tfrac{1}{\sqrt{d_1}}\left(\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)U_{1i}^{(2)} + W_{1i}^{(2)}\sigma''(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\tfrac{1}{\sqrt{d_0}}U_i^{(1)}x\right)\tfrac{1}{\sqrt{d_0}} x_{j_1} \end{align*}

Therefore we have:

\begin{align*} &\|(D_WD_{W^{(1)}} f_x(W))U\|_F^2 = \sum_{i=1}^{d_1} \sum_{j=1}^{d_0} ((D_WD_{W_{ij}^{(1)}} f_x(W)) U)^2 \\ &= \sum_{i=1}^{d_1} \sum_{j=1}^{d_0} \left(\tfrac{1}{\sqrt{d_1}}\left(\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)U_{1i}^{(2)} + W_{1i}^{(2)}\sigma''(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\tfrac{1}{\sqrt{d_0}}U_i^{(1)}x\right)\tfrac{1}{\sqrt{d_0}} x_j\right)^2 \\ &= \frac{1}{d_1}\sum_{i=1}^{d_1} \left(\sigma'(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)U_{1i}^{(2)} + W_{1i}^{(2)}\sigma''(\tfrac{1}{\sqrt{d_0}}W_i^{(1)}x)\tfrac{1}{\sqrt{d_0}}U_i^{(1)}x\right)^2 \\ &\leq \frac{1}{d_1}\sum_{i=1}^{d_1} \left(C|U_{1i}^{(2)}| + |W_{1i}^{(2)}|\cdot C \cdot |\tfrac{1}{\sqrt{d_0}}U_i^{(1)}x|\right)^2 \\ &\leq C^2\frac{1}{d_1}\sum_{i=1}^{d_1} \left(|U_{1i}^{(2)}| + \|W^{(2)}\|_\infty|\tfrac{1}{\sqrt{d_0}}U_i^{(1)}x|\right)^2 \\ &\leq C^2\frac{1}{d_1}\left(\|U^{(2)}\|_F^2 + 2\|W^{(2)}\|_\infty\|U^{(2)}\|_F\|U^{(1)}\|_F + \|W^{(2)}\|_\infty^2 \|U^{(2)}\|_F^2\right) \\ &= C^2\frac{1}{d_1}\left(\|U^{(2)}\|_F + \|W^{(2)}\|_\infty\|U^{(1)}\|_F\right)^2 \\ &\leq C^2\tfrac{1}{d_1}\left(1 + \|W^{(2)}\|_\infty\right)^2 \\ \end{align*}

Therefore the overall squared Frobenius norm is bounded by:

\begin{align*} \|(D^2f_a(W))U\|_F^2 &= \|(D_WD_{W^{(2)}} f_x(W))U\|_F^2 + \|(D_WD_{W^{(1)}}f_x(W))U\|_F^2 \\ &= \tfrac{1}{d_1} C^2(1+(1+\|W^{(2)}\|_\infty)^2) \\ &\leq 2C^2\tfrac{1}{d_1} (1+\|W^{(2)}\|_\infty)^2 \end{align*}

which is the theorem. $\square$

Intuition: If you make the MLP extremely wide, then you can still have a $\Theta(1)$ impact on any given input’s output just by changing the weights by an update of size $\Theta(1)$. However, each neuron’s contribution shrinks by $1/d_1$, and curvature only happens for neurons whose individual connections (incoming or outgoing) change by $\Omega(1)$. So only at most $O(1/d_1)$ neurons can have any curvature. Indeed, $(D^2f_a(W)U)U = O(1/d_1)$.

Remark: The conditions we placed on the derivatives of $\sigma$ allow it to include the sigmoid, GELU, arbitrarily-smoothed-ReLU, and ReLU$^2$ activations, which is essentially everything used in practice.

Setup: optimization trajectories

Let $W$ be the weights of the MLP at initialization. Then we define an optimization trajectory to be a series of weight updates $U_1, \dots, U_T$, where each update is given by some linear mixture of the weight-output gradients of each input in the dataset. In particular, we assume that

$$U_{t+1} = G(W + U_1 + \dots + U_t)\alpha^{(t)}$$

for some weighting $\alpha^{(t)} \in {\mathbb R}^N$, which may be a function of the current weights. For example, $\alpha^{(t)}$ might be the output-loss derivatives for each of the examples, for some loss function.

We also write

$$\hat y^{(t)} := f_X(W + U_1 + \dots + U_t)$$

to denote the outputs of the model after the $t$th update step.

Note that the number of steps $T$ may also be a function of the width or dataset size.

We now begin proving smoothness lemmas about this trajectory. Each holds almost-surely. We use the assumption that $\|x\|_2 \leq \sqrt d_0$ throughout, which for example implies $\|\mathrm{NTK}(\tfrac{1}{d_0} X^\top X)\|_\infty = O(1)$.

Smoothness lemmas

Lemma S0. If $N = O(\sqrt d_1)$ and $\|\alpha^{(1)}\|_1 + \dots + \|\alpha^{(T)}\|_1 = \tilde O(N)$, then every weight along the optimization trajectory satisfies $\|W^{(2)}\|_\infty = \tilde O(1)$.

Proof. The satisfaction of this condition at initialization is given by elementary properties of Gaussian variables.

Now let $x$ be any input with $\|x\| \leq \sqrt d_0$. And let $W$ be any weight. Then we have:

\begin{align*} \|\nabla_{W^{(2)}} f_x(W)\|_\infty &= \|\tfrac{1}{\sqrt d_1}\sigma(\tfrac{1}{\sqrt d_0}W^{(1)}x)\|_\infty \\ &\leq \tfrac{1}{\sqrt d_1}\max_{1 \leq i \leq d_1}\|W_i^{(1)}\|_2 \end{align*}

and

\begin{align*} \max_{1 \leq i \leq d_1} \|\nabla_{W_i^{(1)}} f_x(W)\|_2 &= \max_{1 \leq i \leq d_1} \|\tfrac{1}{\sqrt d_1}W_{1i}^{(2)}\tfrac{1}{\sqrt d_0}x\|_2 \\ &\leq \tfrac{1}{\sqrt d_1}\|W^{(2)}\|_\infty \end{align*}

Therefore, the condition $\max(\|W^{(2)}\|_\infty, \max_{1 \leq i \leq d_1}\|W_i^{(1)}\|_2) = \tilde O(1)$, is preserved by any update of the form $G(W)\alpha$ where $\alpha \in {\mathbb R}^N$ satisfies $\|\alpha\|_1 = \tilde O(N)$ and $N = O(\sqrt d_1)$. In particular, we can perform an arbitrary $T$ such updates, and still preserve the property. In particular, we will preserve $\|W^{(2)}\|_\infty = \tilde O(1)$. $\square$

Given Lemma S0, in all future lemmas, when we write $\sup_{U : \dots}$, the conditions shall be understood to include $\|U^{(2)}\|_\infty \leq \tilde O(1)$. In particular, $U$ can be understood to be a supremum over all possible updates in a trajectory (including sums of updates). Similarly, lemmas involving $\alpha$ shall hold uniformly for all $\alpha$ such that $\|\alpha^{(1)}\|_1 + \dots + \|\alpha^{(T)}\|_1 = \tilde O(N)$, (i.e., for a fixed function in that growth class).

Lemma S1. Let $W$ be the weights at initialization. Then almost-surely we have both:

$$\sup_{x : \|x\|^2 \leq d_0, U: \|U\|_F \leq \tilde o(d_1^\gamma)}\left|f_x(W + U) - \left(f_x(W) + (Df_x(W))U\right)\right| = \tilde o(d_1^{\gamma-1/2})$$
$$\sup_{x : \|x\|^2 \leq d_0, U: \|U\|_F \leq \tilde o(d_1^\gamma)}\|\nabla f_x(W + U) - \nabla f_x(W)\|_F = \tilde o(d_1^{\gamma-1/2})$$

Proof. For the first statement, We have:

\begin{align*} \sup_{U : \|U\|_F \leq o(d_1^\gamma)} &\left\|f_x(W + U) - \left(f_x(W) + (Df_x(W))U\right)\right\| \\ &\leq \sup_U\sup_{\lambda \in [0, 1]}\lambda^2 ((D^2f_x(W + \lambda U))U)U \\ &\leq \sup_U\sup_{\lambda \in [0, 1]} \|D^2f_a(W + \lambda U)\|_* \|U\|_F \\ &\leq \sup_U\sup_{\lambda \in [0, 1]} O(d_1^{-1/2})\|W + \lambda U\|_\infty \|U\|_F \\ &= \sup_U\sup_{\lambda \in [0, 1]} O(d_1^{-1/2})(\|W^{(2)}\|_\infty + \|U^{(2)}\|_\infty) \|U\|_F \\ &= \sup_U O(d_1^{-1/2})(\tilde O(1) + \tilde O(1)) \tilde o(d_1^\gamma) \\ &= \tilde o(d_1^{\gamma-1/2}) \end{align*}

Where we use the Hessian theorem and obtain $\|W^{(2)}\|_\infty = \tilde O(1)$, where $\tilde O$ hides logarithmic factors, from a preliminary lemma.

For the second statement, we have:

\begin{align*} \|\nabla f_x(W + U) - \nabla f_x(W)\|_F &\leq \sup_{0 \leq \lambda \leq 1}\|D^2f_x(W + \lambda U)\|_* \|U\|_F \\ &\leq O(d_1^{-1/2})(\|W\|_\infty + \|U\|_\infty)\|U\|_F \\ &\leq \tilde o(d_1^{\gamma-1/2}). \end{align*}

$\square$

In addition, as long as we stay within this radius, the dot products between gradients will stay close to what they would have been at initialization.

Lemma S2. Almost-surely:

$$\sup_{U: U : \|U\|_F \leq o(d_1^\gamma)}\|K(W+U) - K(W)\|_\infty = \tilde o(d_1^{\gamma-1/2})$$

Proof. Each entry of $K(W+U) - K(W)$ is a difference of the form

$$\langle \nabla f_x(W + U), \nabla f_{\tilde x}(W + U) \rangle - \langle \nabla f_x(W), \nabla f_{\tilde x}(W)\rangle$$

for some pair $(x, \tilde x)$ of columns of $X$. This is bounded by

\begin{align*} &|\langle \nabla f_x(W + U), \nabla f_{\tilde x}(W + U) \rangle - \langle \nabla f_x(W), \nabla f_{\tilde x}(W) \rangle| \\ &= \Big|\left(\langle \nabla f_x(W + U), \nabla f_{\tilde x}(W + U) \rangle - \langle \nabla f_x(W + U), \nabla f_{\tilde x}(W) \rangle\right) \\ &\quad+ \left(\langle \nabla f_x(W + U), \nabla f_{\tilde x}(W) \rangle - \langle \nabla f_x(W), \nabla f_{\tilde x}(W) \rangle\right)\Big| \\ &= \Big|\langle \nabla f_x(W + U), \nabla f_{\tilde x}(W + U) - \nabla f_{\tilde x}(W) \rangle + \langle \nabla f_x(W + U) - \nabla f_x(W), \nabla f_{\tilde x}(W) \rangle\Big| \\ &\leq \|\nabla f_x(W + U)\|\|\nabla f_{\tilde x}(W + U) - \nabla f_{\tilde x}(W)\| + \|\nabla f_x(W + U) - \nabla f_x(W)\|\|\nabla f_{\tilde x}(W)\| \\ &\leq \left(\|\nabla f_x(W)\| + \|\nabla f_x(W + U) - \nabla f_x(W)\|\right)\|\nabla f_{\tilde x}(W + U) - \nabla f_{\tilde x}(W)\| \\ &\quad+ \|\nabla f_x(W + U) - \nabla f_x(W)\|\|\nabla f_{\tilde x}(W)\| \\ &\leq \left(\|\nabla f_x(W)\| + o(d_1^{\gamma-1/2})\right)o(d_1^{\gamma-1/2}) + o(d_1^{\gamma-1/2})\|\|\nabla f_{\tilde x}(W)\| \\ &= \left(\|\nabla f_x(W)\| + \|\nabla f_{\tilde x}(W)\|\right)o(d_1^{\gamma-1/2}) \end{align*}

where we used Lemma S1, assuming that $\|\nabla f_x(W)\| = \Omega(1)$.

Using the NTK convergence theorem, we have $\|\nabla f_x(W)\|^2 = \mathrm{NTK}(\frac{1}{d_0}X^\top X) + \tilde O(d_1^{-1/2})$, where the assumption that inputs have bounded norm implies that the entries of the NTK are bounded by a constant. Therefore, $\|\nabla f_x(W)\| = O(1)$, uniformly across the columns, and so the asymptotic limit is just $o(d_1^{-1/2})$. $\square$

Lemma S3. Uniformly across all gradient weightings $\beta \in {\mathbb R}^N$, we have:

$$\sup_{U : \|U\|_F \leq o(d_1^{1/2})} \|G(W+U)\beta\|_F = \|\beta\|_1O(1)$$

Proof.

\begin{align*} \|G(W+U)\beta\|_F^2 &= (G(W+U)\beta)^\top (G(W+U)\beta) \\ &= \beta^\top K(W+U)\beta \\ &\leq \|\beta\|_1^2 \|K(W+U)\|_\infty \\ &= \|\beta\|_1^2 (\|K_\infty\|_\infty + \tilde O(d_1^{-1/2}) + \tilde O(d_1^{\gamma-1/2})) \\ &= \|\beta\|_1^2O(1) \end{align*}

where we used Lemma S2 to control $\|K(W+U) - K(W)\|_\infty$ by $\tilde O(d_1^{\gamma-1/2})$ with $\gamma = 1/2$, and the main NTK convergence theorem to control $\|K(W) - K_\infty\|_\infty$ by $\tilde O(d_1^{-1/2})$. $\square$

S4, in which we lose square-root scaling

Lemma S4. Assume that $N = o(d_1^\gamma)$. Then uniformly across all $\beta \in {\mathbb R}^N$, we have:

$$\sup_{U: \|U\|_F \leq o(d_1^\gamma)} \|f_X(\widetilde{W}) - (f_X(W+U) + K(W)\beta)\|_\infty = (1 + \|\beta\|_1)\tilde o(d_1^{\gamma-1/2})$$

where $\widetilde{W} := W+U+G(W+U)\beta$ are the weights after taking a gradient step weighted by $\beta$.

Proof.

First, observe that Lemma S3 implies $\|G(W+U)\beta\|_F = \tilde O(N) = \tilde o(d_1^\gamma)$. Therefore the entire difference from initialization has $\|U + G(W+U)\beta\|_F = \tilde o(d_1^\gamma)$, so Lemma S1 applies, proving that:

$$\|f_X(\widetilde{W}) - (f_X(W) + G(W)^\top(U+G(W+U)\beta))\|_\infty = \tilde o(d_1^{\gamma-1/2})$$
$$\|f_X(W+U) - (f_X(W) + G(W)^\top U)\|_\infty = \tilde o(d_1^{\gamma-1/2})$$

which combine to yield

$$\|f_X(\widetilde{W}) - (f_X(W+U) + G(W)^\top G(W+U)\beta)\|_\infty = \tilde o(d_1^{\gamma-1/2})$$

so it remains to prove that $\|G(W)^\top G(W+U)\beta - K(W)\beta\|_\infty = \|\beta\|_1\tilde o(d_1^{\gamma-1/2})$.

Define $\beta := G(W)^\top G(W+U)\beta$. Then we have

\begin{align*} |(\beta - K(W)\beta)_{n_1}| &= |G(W)_{:n_1}^\top (G(W+U) - G(W))\beta| \\ &\leq \|G(W)_{:n_1}\|_F\|(G(W+U) - G(W))\beta\|_F \\ &= O(1)\|(G(W+U) - G(W))\beta\|_F \\ &= O(1)\left\|\sum_{n_2=1}^N \beta_{n_2}(\nabla f_{x^{(n_2)}}(W+U) - \nabla f_{x^{(n_2)}}(W))\right\|_F \\ &\leq O(1) \sum_{n_2=1}^N |\beta_{n_2}| \|\nabla f_{x^{(n_2)}}(W+U) - \nabla f_{x^{(n_2)}}(W)\|_F \\ &\leq O(1)\|\beta\|_1 \max_{n_2 \in \{1, \dots, N\}} \|\nabla f_{x^{(n_2)}}(W+U) - \nabla f_{x^{(n_2)}}(W)\|_F \\ &= \|\beta\|_1\tilde o(d_1^{\gamma-1/2}) \end{align*}

by Lemma S1. This was uniform across $n_1$, hence the $L^\infty$ norm is also $\|\beta\|_1\tilde o(d_1^{\gamma-1/2})$. $\square$

Remark: The last series of inequalities is essentially tight if, for example, every input is the same.

Trajectory linearization theorem

Denote the NTK by $K_\infty := \mathrm{NTK}(\tfrac{1}{d_0}X^\top X)$.

Theorem. If $N = \tilde o(d_1^{1/4})$, $T = \tilde O(N)$ and $\max_{1 \leq t \leq T}\|\alpha^{(t)}\|_1 = \tilde O(N/T)$, then uniformly for all trajectories and timestep pairs $0 \leq t_1 < t_2 \leq T$ we have:

$$\|(\hat y^{(t_2)} - \hat y^{(t_1)}) - K_\infty(\alpha^{(t_1+1)} + \dots + \alpha^{(t_2)}))\|_\infty = (t_2-t_1)\tilde o(1/T)$$

Proof. For any $0 \leq t_1 < t_2 \leq T$, define $\beta := \alpha^{(t_1+1)} + \dots + \alpha^{(t_2)}$. Then by the NTK convergence theorem we have uniformly

\begin{align*} \|K(W)\beta - \mathrm{NTK}(\tfrac{1}{d_0}X^\top X)\beta\|_\infty &\leq \|K(W) - \mathrm{NTK}(\tfrac{1}{d_0}X^\top X)\|_\infty\|\beta\|_1 \\ &= \tilde O(d_1^{-1/2}) \tilde O(N) \\ &= \tilde o(d_1^{-1/4}) = \tilde o(1/T). \end{align*}

In addition, we have

\begin{align*} &\|(\hat y^{(t_2)} - \hat y^{(t_1)}) - K(W)(\alpha^{(t_1+1)} + \dots + \alpha^{(t_2)}))\|_\infty \\ &\quad\leq \sum_{s=t_1+1}^{t_2} \|(\hat y^{(s)} - \hat y^{(s-1)}) - K(W)\alpha^{(s)}\|_\infty \\ &\quad= \sum_{s=t_1+1}^{t_2} \|(f_X(\widetilde{W}) - f_X(W + U) - K(W)\alpha^{(s)}\|_\infty \\ &\quad\leq \sum_{s=t_1+1}^{t_2} (1 + \|\alpha^{(s)}\|_1)\tilde o(d_1^{1/4-1/2}) \\ &\quad= (t_2-t_1)(1 + \tilde O(N/T))\tilde o(d_1^{-1/4}) \\ &\quad= (t_2-t_1)(\tilde o(d_1^{-1/4}) + \tilde o(1/T)) \\ &\quad= (t_2-t_1)(\tilde o(1/T) + \tilde o(1/T)) = (t_2-t_1)\tilde o(1/T) \end{align*}

where we define $U := U_1 + \dots + U_{s-1}$ and $\widetilde{W} := W + U + G(W + U)\alpha^{(s)}$ so that Lemma S4 yields the second inequality, because we have uniformly

$$\|U\|_F \leq \sum_{s=1}^t \|U_s\|_F = \sum_{s=t_1+1}^{t_2} \|\alpha^{(s)}\|_1 \tilde O(1) = \tilde O(N/T)O(T) = \tilde o(d_1^{1/4})$$

by Lemma S3. So combining these yields the theorem. $\square$

Application to square-loss gradient descent

Now suppose instead that $y \in {\mathbb R}^N$ is a vector of linear regression targets, with loss

$${\mathcal L}(W) = \tfrac12 \|f_X(W) - y\|_2^2$$

Then it can be verified that he gradient descent trajectory with learning rate $\eta$ is given by

$$\alpha^{(t+1)} := \eta (y - \hat y^{(t)})$$

We assume that the maximum regression target $\|y\|_\infty = \tilde O(1)$ does not grow super-logarithmically with the dataset size, e.g., $y$ can be sampled as Gaussians, or any bounded distribution.

Theorem. If $N = \tilde o(d_1^{-1/4})$, $T = \tilde O(N)$ and $0 < \eta \leq \mathrm{NTK}(\kappa=1)/N$, then uniformly for all timesteps $1 \leq t \leq T$ we have:

$$\tfrac1N\|(\hat y^{(t)} - y) - (I - \eta K_\infty)^t(\hat y^{(0)} - y)\|_2^2 = \tilde o(1)$$

Proof. We first analyze the spectral norm $\|I - \eta K_\infty\|_*$. Observe that $\|K_\infty\|_\infty \leq \mathrm{NTK}(\kappa=1)$, so $\|\eta K_\infty\|_\infty \leq 1/N$. Therefore, $0 < \|\eta K_\infty\|_* \leq 1$, where we know it is positive since $K_\infty$ must be nonzero. Therefore $0 \leq \|I - \eta K_\infty\|_\infty < 1$ as well, since $K_\infty$ is positive semidefinite. (To see that $K_\infty$ is PSD, note that by definition, it can be arbitrarily well-approximated by $G^\top G$ where $G$ are the gradients from a wide network)

We next observe that each entry $\|\hat y^{(0)} - y\|_\infty = \tilde O(1)$, as usual due to standard properties of Gaussian variables and our assumption that $\|y\|_\infty = \tilde O(1)$. Therefore, in particular, $\|\hat y^{(0)} - y\|_2 = \tilde O(\sqrt N)$.

Now inductively assume that uniformly across $0 \leq s \leq t$, we have

$$\|(\hat y^{(s)} - y) - (I - \eta K_\infty)^s(\hat y^{(0)} - y)\|_2 = \sqrt N\tilde o(1)$$

that is, assume the statement holds for all such $s$, such that we can replace $\tilde o(1)$ with a single function which is in $\tilde o(1)$.

The base case is trivial. We will prove that the statement holds for $0 \leq s \leq t+1$ uniformly as well. First, observe that the inductive assumption implies that for $1 \leq s \leq t$ we have uniformly

\begin{align*} \|\hat y^{(s)} - y\|_1 &\leq \sqrt N \|\hat y^{(s)} - y\|_2 \\ &\leq \sqrt N\Big(\|(\hat y^{(s)} - y) - (I - \eta K_\infty)^s(\hat y^{(0)} - y)\|_2 + \|(I - \eta K_\infty)^s(\hat y^{(0)} - y)\|_2\Big) \\ &\leq N\tilde o(1) + \sqrt N\|I - \eta K_\infty\|_*^s\|\hat y^{(0)} - y\|_2 \\ &\leq \tilde o(N) + \sqrt N \tilde O(\sqrt N) \\ &= \tilde O(N) \end{align*}

hence using our assumption that $\eta = \tilde O(1/N)$, we obtain that uniformly

$$\|\alpha^{(s)}\|_1 = \|\eta (y - \hat y^{(s)})\|_1 = \tilde O(1/T)\tilde O(N) = \tilde O(N/T)$$

so we can therefore apply that trajectory linearization theorem to obtain that

$$\|(\hat y^{(s)} - \hat y^{(s-1)}) - \eta K_\infty(y - y^{(s-1)})\|_\infty = \|(\hat y^{(s)} - \hat y^{(s-1)}) - K_\infty\alpha^{(s)}\|_\infty = \tilde o(1/T)$$

uniformly across $1 \leq s \leq t$. This allows us to control the $L^2$ norm via the following.

\begin{align*} &\|(\hat y^{(t)} - y) - (I - \eta K_\infty)^t(\hat y^{(0)} - y)\|_2 \\ &\quad\quad\leq \sum_{s=1}^t \|(I - \eta K_\infty)^{t-s}(\hat y^{(s)} - y) - (I - \eta K_\infty)^{t-s+1}(\hat y^{(s-1)} - y)\|_2 \\ &\quad\quad\leq \sum_{s=1}^t \|I - \eta K_\infty\|_*^{t-s}\|(\hat y^{(s)} - y) - (I - \eta K_\infty)(\hat y^{(s-1)} - y)\|_2 \\ &\quad\quad= \sum_{s=1}^t \|I - \eta K_\infty\|_*^{t-s}\|(\hat y^{(s)} - \hat y^{(s-1)}) - \eta K_\infty(y - \hat y^{(s-1)})\|_2 \\ &\quad\quad\leq \sum_{s=1}^t \|I - \eta K_\infty\|_*^{t-s}\sqrt N\|(\hat y^{(s)} - \hat y^{(s-1)}) - \eta K_\infty(y - \hat y^{(s-1)})\|_\infty \\ &\quad\quad= \sum_{s=1}^t \|I - \eta K_\infty\|_*^{t-s}\sqrt N\tilde o(1/T) \\ &\quad\quad= \sqrt N \cdot \tilde o(1)(1 - \|I - \eta K_\infty\|_*)^{-1} \\ &\quad\quad= \sqrt N \cdot \tilde o(1) \end{align*}

Therefore, the induction carries through and we obtain uniformly

$$\|(\hat y^{(t)} - y) - (I - \eta K_\infty)^t(\hat y^{(0)} - y)\|_2 = \sqrt N\tilde o(1)$$

for all $1 \leq t \leq T$, which is equivalent to the theorem statement. $\square$

Rate of convergence

In addition to the setup of the previous theorem, assume that the smallest eigenvalue of $K_\infty$ is $c > 0$. This implies that $\|I - \eta K_\infty\|_* \leq 1 - c/N$ where $c’ = c\mathrm{NTK}(\kappa=1)$. Then using the theorem we have

\begin{align*} \|\hat y^{(t)} - y\|_2 &\leq \|(\hat y^{(t)} - y) - (I - \eta K_\infty)^t(\hat y^{(0)} - y)\|_2 + \|(I - \eta K_\infty)^t(\hat y^{(0)} - y)\|_2 \\ &\leq \sqrt N \tilde o(1) + \|I - \eta K_\infty\|_*^t \tilde O(\sqrt N) \\ &= \tilde O(\sqrt N) (\tilde o(1) + \|I - \eta K_\infty\|_*^t) \\ &\leq \tilde O(\sqrt N) (\tilde o(1) + (1 - c/N)^t) \\ &\leq \tilde O(\sqrt N) (\tilde o(1) + e^{-tc/N}) \\ \end{align*}

Therefore, if we let $T = \omega(N)$ grow faster than $N$, while still validly satisfying $T = \tilde O(N)$ (e.g., $T = N\log N$), then we get

$$\|\hat y^{(T)} - y\|_2 = \tilde O(\sqrt N)(\tilde o(1) + e^{-c\omega(1)}) = \tilde o(\sqrt N) o(1) = \tilde o(\sqrt N)$$

which is equivalent to

$$\tfrac1N\|\hat y^{(T)} - y\|_2^2 = \tilde o(1)$$

that is, that the average square loss decreases to zero as we scale everything up.

However, this assumption is not necessarily realistic. It is easily possible that as we scale up the data, the smallest eigenvalue goes to zero. For example, if there are any duplicates then this will be the case. If there are duplicates, then as in any regression problem, we will have to hope that their regression targets are also equal; otherwise the problem is not perfectly solvable.

On the other hand, if all of the points are orthogonal, as is assumed in some theory papers about this topic, then for essentially any nontrivial activation function the condition will be satisfied.

Convergence theorem. Given $N = O(\mathrm{width}^{1/4})$ orthogonal inputs, and arbitrary bounded regression targets, in the limit as we scale everything up, an MLP with one hidden layer will perfectly solve the regression after $\omega(N)$ steps of gradient descent.

It seems tempting to think that, because the inputs are orthogonal, we could realisticly only use $\omega(1)$ steps of gradient descent with a constant learning rate. However, if the targets are all-positive, then this will still lead to diverging oscillation, due to the fact that $\mathrm{NTK}(\kappa=0) > 0$.

Appendix

Dual of an activation

Definition

Definition. For any activation function $\sigma: {\mathbb R} \to {\mathbb R}$, its dual $\mathring{\sigma} : {\mathbb R}^{N \times N} \to {\mathbb R}^{N \times N}$ is

$$\mathring{\sigma}(\Lambda) = {\mathbb E}_{z \sim {\mathcal N}(0, \Lambda)}\left[\sigma(z)\sigma(z)^\top\right]$$

That is, the expected outer product of $\sigma(z)$ where $z \in {\mathbb R}^N$ is centered Gaussian with covariance matrix $\Lambda \in {\mathbb R}^{N \times N}$. If $\Lambda$ is not positive semidefinite, the output is undefined.

Intuition: The dual activation describes how the activation function transforms the statistics of Gaussian distributions.

We overload the definition of $\mathring{\sigma}$ to apply to all $N \geq 2$ at once, so that the following proposition statement makes sense.

Proposition. For any covariance matrix $\Lambda \in {\mathbb R}^{N \times N}$, the outputs of $\mathring{\sigma}$ are determined by its outputs on $2\times2$ covariance matrices via:

$$\mathring{\sigma}(\Lambda)_{ij} = \mathring{\sigma}\left(\begin{smallmatrix}\Lambda_{ii} & \Lambda_{ij} \\ \Lambda_{ji} & \Lambda_{jj}\end{smallmatrix}\right)_{12}$$

Proof.

\begin{align*} {\mathbb E}_{z \sim {\mathcal N}(0, \Lambda)}\left[\sigma(z)\sigma(z)^\top\right]_{ij} &= {\mathbb E}_{z \sim {\mathcal N}(0, \Lambda)}\left[\sigma(z)_i\sigma(z)_j\right] \\ &= {\mathbb E}_{z, \tilde z \sim {\mathcal N}\left(0, \begin{smallmatrix}\Lambda_{ii} & \Lambda_{ij} \\ \Lambda_{ji} & \Lambda_{jj}\end{smallmatrix}\right)}\left[\sigma(z)\sigma(\tilde z)\right] \\ &= \mathring{\sigma}\left(\begin{smallmatrix}\Lambda_{ii} & \Lambda_{ij} \\ \Lambda_{ji} & \Lambda_{jj}\end{smallmatrix}\right)_{12} \end{align*}

$\square$

Proposition. For any PSD input $\Lambda \in {\mathbb R}^{N \times N}$, and any activation $\sigma: {\mathbb R} \to {\mathbb R}$, $\mathring{\sigma}(\Lambda)$ is positive semidefinite.

Proof. It’s a covariance matrix of a random vector with itself, which is always PSD.

We further overload the definition by defining $\mathring{\sigma}: [-1, 1] \to {\mathbb R}$ via:

$$\mathring{\sigma}(\kappa) = \mathring{\sigma}\left( \begin{smallmatrix} 1 & \kappa \\ \kappa & 1 \end{smallmatrix}\right).$$

This version can be consistently applied elementwise in the case that $\Lambda$ has unit diagonal.

Proposition. If $\Lambda \in {\mathbb R}^{N \times N}$ is a covariance matrix satisfying $\Lambda_{ii} = 1$, then

$$\mathring{\sigma}(\Lambda)_{ij} = \mathring{\sigma}(\Lambda_{ij})$$

Proof. Follows easily from the previous proposition.

ReLU case

Theorem. If $\sigma(x) = \sqrt 2 \max(0, x)$, then

\begin{align*} \mathring{\sigma}(\kappa) &= \tfrac{1}{\pi}\sqrt{1-\kappa^2} + \kappa(1 - \tfrac2\pi\sin^{-1}(\sqrt{(1-\kappa)/2})) \\ \mathring{\sigma}'(\kappa) &= \tfrac2\pi\sin^{-1}(\sqrt{(1+\kappa)/2}) \end{align*}

Proof. A bunch of calculus.

Gaussians are almost bounded

Proposition. Let $X_1, X_2, \dots$ be IID Gaussian. Then

$$P\left(\max_{i=1, \dots, n} X_i^2 = \tilde O(1)\right) = 1$$

Proof.

\begin{align*} P\left(\max_{i=1, \dots, n} X_i^2 \geq \log^{3/2}n\quad \text{i.o.}\right) &= P\left(X_n^2 \geq \log^{3/2}n\quad \text{i.o.}\right) \\ &\leq 1\left\{\sum_{n=1}^\infty P(|X_n| \geq \log^{3/4}n) = \infty\right\} \\ &\leq 1\left\{\sum_{n=1}^\infty \exp(-O((\log^{3/4}n)^2)) = \infty\right\} \\ &\leq 1\left\{\sum_{n=1}^\infty O(n^{-3/2}) = \infty\right\} \\ &\leq 0. \end{align*}

$\square$

Remark: Check a standard textbook for the complete proof of this fact.

Generic sub-exponential large deviation bound

Theorem. Suppose that $Y$ satisfies ${\mathbb E}[|Y|^k] \leq c_kk!$ for some $c > 0$. And let $\mu = {\mathbb E}[Y]$, and $S := \sum_{n=1}^N Y_n$ where $Y_n$ is an IID copy of $Y$. Then for every $a \in [0, c]$, we have

$$P(|S/N - \mu| \geq a) \leq e^{-N(0.08(a/c)^2)}$$

Proof. Suppose that a positive variable $Y$ satisfies ${\mathbb E}[|Y|^k] \leq c^kk!$ for some $c > 0$. Then certainly the variable $Z := Y - {\mathbb E}[Y]$ satisfies ${\mathbb E}[Z^k] \leq c^kk!$ and ${\mathbb E}[Z] = 0$. Therefore for $\theta > 0$

$${\mathbb E}[e^{\theta Z}] = \sum_{k=0}^\infty \theta^k{\mathbb E}[Z^k]/k! \leq 1 + \sum_{k=2}^\infty (c\theta)^k \leq 1 + \frac{(c\theta)^2}{1 - c\theta}$$

whenever $c\theta < 1$, that is, $\theta < 1/c$.

Now let $S := \sum_{n=1}^N Z_n$ where $Z_1, Z_2, \dots$ are IID copies of $Z$. Then we have

$${\mathbb E}[e^{\theta S}] = {\mathbb E}[e^{\theta Z}]^N \leq e^{N(c\theta)^2/(1-c\theta)}$$

Therefore:

\begin{align*} P(S \geq Na) &\leq \inf_{\theta > 0}\frac{{\mathbb E}[e^{\theta S}]}{e^{\theta Na}} \\ &\leq \inf_{\theta > 0} e^{N(c\theta)^2/(1-c\theta) - N \theta a} \\ &= e^{-N(\sup_{\theta > 0}(\theta a - (c\theta)^2/(1-c\theta)))} \\ \end{align*}

which can be solved by setting $(\theta a - (c\theta)^2/(1-c\theta))’ = 0$, that is:

$$a - \frac{(1-c\theta)(2c \theta)c - (c\theta)^2\cdot(-c)}{(1-c\theta)^2} = 0$$
$$a(1-c\theta)^2 = (1-c\theta)(2c \theta)c - (c\theta)^2\cdot(-c)$$
$$a - 2ca\theta + ac^2\theta^2 = 2c^2\theta - c^3\theta^2$$
$$(c^3 + ac^2)\theta^2 - 2(c^2 + ac)\theta + a = 0$$
$$\theta^2 - 2(1/c)\theta + a/(c^2(c+a)) = 0$$

QUADRATIC EQUATION $-B \pm \sqrt{B^2 - C}$ for $x^2 - 2Bx + C$.

$$\theta = (1/c) \pm \sqrt{1/c^2 - a/(c^2(c+a))}$$
$$\theta = (1/c)\left(1 \pm \sqrt{c/(c+a)}\right)$$

We require $\theta < 1/c$ for the series to converge, so the solution is

$$\theta^* = (1/c)(1 - \sqrt{\tfrac{c}{a+c}})$$

which yields

\begin{align*} \sup_{\theta > 0}(\theta a - (c\theta)^2/(1-c\theta)) &= \theta^*a - (1-\sqrt{\tfrac{c}{a+c}})^2/\sqrt{\tfrac{c}{a+c}} \\ &= \tfrac{a}{c}(1 - \sqrt{\tfrac{c}{a+c}}) - (\sqrt{\tfrac{a+c}{c}} - 2 + \sqrt{\tfrac{c}{a+c}}) \\ &= 2 + \tfrac{a}{c} - \tfrac{a}{c}\sqrt{\tfrac{c}{a+c}} - \sqrt{\tfrac{a+c}{c}} - \sqrt{\tfrac{c}{a+c}} \\ &= 2 + \tfrac{a}{c} - (1 + \tfrac{a}{c})\sqrt{\tfrac{c}{a+c}} - \sqrt{\tfrac{a+c}{c}} \\ &= 2 + \tfrac{a}{c} - \tfrac{a+c}{c}\sqrt{\tfrac{c}{a+c}} - \sqrt{\tfrac{a+c}{c}} \\ &= 2 + \tfrac{a}{c} - 2\sqrt{\tfrac{a+c}{c}} \\ &= 2 + \tfrac{a}{c} - 2\sqrt{1 + \tfrac{a}{c}} \\ \end{align*}

which can be controlled by the observation that if we define $g(x) = (2 + x) - 2\sqrt{1+x}$, then $g’(x) = 1 - (1+x)^{-1/2}$ and $g’’(x) = (1/2)(1+x)^{-3/2}$. If we assume that $x \in [0, 1]$, then this is at least $g’’(x) \geq (1/2) \cdot 2^{-3/2} \geq 0.16$. Therefore if $x \in [0, 1]$ then $g’(x) \geq g’(0) + 0.16x$ and hence $g(x) \geq g(0) + xg’(0) + 0.16x^2/2 = 0.08x^2$.

Therefore we have

$$\sup_{\theta > 0}(\theta a - (c\theta)^2/(1-c\theta)) \geq 0.08(a/c)^2$$

And so, putting it all together, we get

$$P(S \geq Na) \leq e^{-N(0.08(a/c)^2)}$$

$\square$

Remark: I have been informed by GPT-o1 that what I’ve done here could also be more easily accomplished by invoking something called the Bernstein inequality for sub-exponential variables.

The remaining two sections are not depended upon by anything else in this note.

Linear regression dynamics

Suppose that we are solving a linear regression problem with dataset $X \in {\mathbb R}^{N \times d}$ and targets $y \in {\mathbb R}^N$ using gradient descent. That is, we want to solve

$$\mathop{\mathrm{arg\,min}\,}_{w \in {\mathbb R}^d}\tfrac12 \|Xw - y\|_2^2$$

using gradient updates

\begin{align*} w' &= w - \eta \nabla_w \tfrac12 \|Xw - y\|_2^2 \\ &= w - \eta X^\top (Xw - y). \\ \end{align*}

Now suppose that we know the kernel matrix $K := XX^\top \in {\mathbb R}^{N \times N}$ of dot products between examples. Then we can write the dynamics of the residuals $r = (y - Xw)$ as

\begin{align*} r' &= (y - Xw') \\ &= (y - X(w - \eta X^\top (Xw - y))) \\ &= (y - Xw - \eta XX^\top (y - Xw)) \\ &= (1 - \eta K)(y - Xw) \\ &= (1 - \eta K)r \end{align*}

Therefore, if we know the kernel $K$ of a linear regression problem, then we can easily predict the dynamics of its residual under gradient descent.

Application to cross-entropy gradient descent trajectory

We now extend the linearization theorem to apply to a trajectory resulting from gradient descent against a logistic loss function. Let $y \in \{-1, +1\}^N$ be a vector of logistic targets for the dataset $X$. And define the loss function ${\mathcal L}: {\mathbb R}^{d_1(1+d_0)} \to [0, \infty)$ via:

$${\mathcal L}(W) := \sum_{n=1}^N \log(1+e^{-y_n f_{x^{(n)}}(W)})$$

It can be verified that the gradient descent trajectory with learning rate $\eta$ is defined by

$$\alpha^{(t+1)} = \eta (y * \mathrm{sigmoid}(-y * \hat y^{(t)}))$$

We can easily apply the theorem to prove that this trajectory is linearized, since we have

$$\|\alpha^{(t+1)}\|_1 = \sum_{n=1}^N \eta |y_n||\mathrm{sigmoid}(-y_nf_{x^{(n)}}(W + U_1 + \dots + U_t))| \leq \eta N$$

hence $\|\alpha^{(t+1)}\|_1 = O(N)$ when $\eta = O(1)$. Therefore, we get the linearization

$$\|(\hat y^{(t+1)} - \hat y^{(t)}) - \eta K_\infty(y * \mathrm{sigmoid}(y * \hat y^{(t)}))\|_\infty = o(1)$$